Evaluating Motion Consistency by Fréchet Video Motion Distance (FVMD)
In this blog post, we introduce a promising new metric for video generative models, Fréchet Video Motion Distance (FVMD), which focuses on the motion consistency of generated videos.
Introduction
Recently, diffusion models have demonstrated remarkable capabilities in high-quality image generation. This advancement has been extended to the video domain, giving rise to text-to-video diffusion models, such as Pika, Runway Gen-2, and Sora
Despite the rapid development of video generation models, research on evaluation metrics for video generation remains insufficient (see more discussion on our blog). For example, FID-VID
Simply put, there is a lack of metrics specifically designed to evaluate the complex motion patterns in generated videos. The Fréchet Video Motion Distance (FVMD) addresses this gap.
The code is available at GitHub.
Fréchet Video Motion Distance (FVMD)
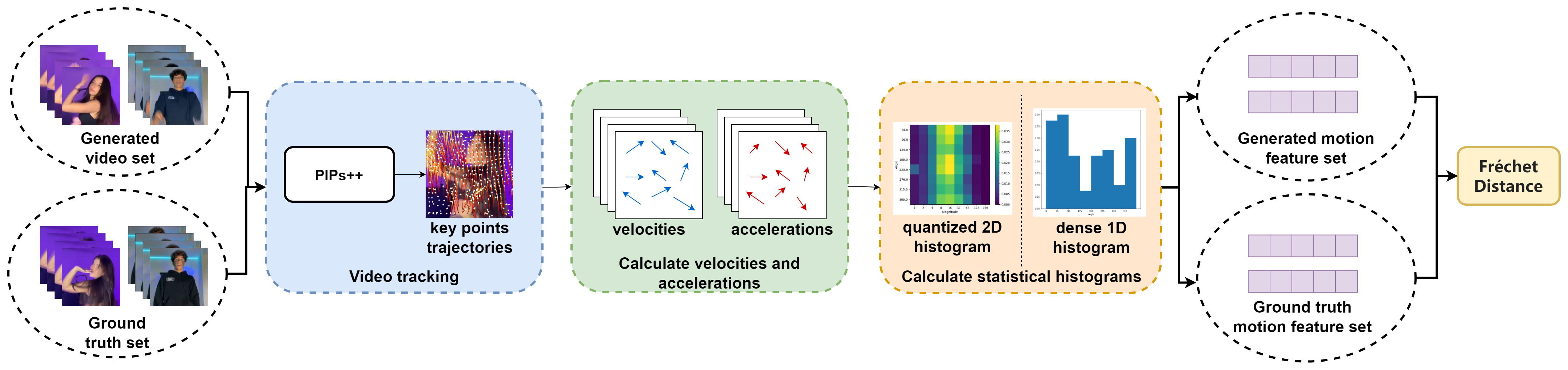
The core idea of FVMD is to measure temporal motion consistency based on the patterns of velocity and acceleration in video movements. First, motion trajectories of key points are extracted using the pre-trained model PIPs++
Video Key Points Tracking
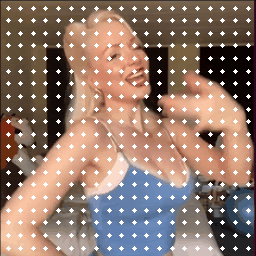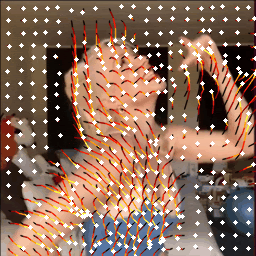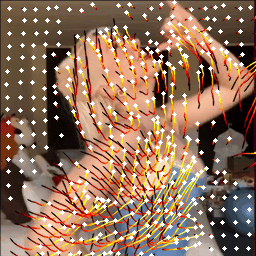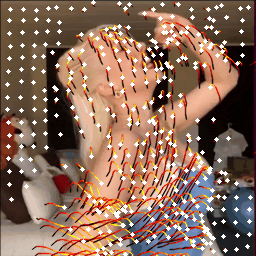

To construct video motion features, key point trajectories are first tracked across the video sequence using PIPs++. For a set of $m$ generated videos, denoted as $\lbrace X^{(i)} \rbrace_{i=1}^m$, the tracking process begins by truncating longer videos into segments of $F$ frames with an overlap stride of $s$. For simplicity, segments from different videos are put together to form a single dataset $\lbrace x_{i} \rbrace_{i=1}^n$. Then, $N$ evenly-distributed target points in a grid shape are queried on the initial frames
Key Points Velocity and Acceleration Fields
FVMD proposes using the velocity and acceleration fields across frames to represent video motion patterns. The velocity field $\hat{V} \in \mathbb{R}^{F \times N \times 2}$ measures the first-order difference in key point positions between consecutive frames with zero-padding:
\[\hat{V} = \texttt{concat}(\boldsymbol{0}_{N\times 2}, \hat{Y}_{2:F} - \hat{Y}_{1:F-1}) \in \mathbb{R}^{F \times N \times 2},\]The acceleration field $\hat{A} \in \mathbb{R}^{F \times N \times 2}$ is calculated by taking the first-order difference between the velocity fields in two consecutive frames, also with zero-padding:
\[\hat{A} = \texttt{concat}(\boldsymbol{0}_{N\times 2}, \hat{V}_{2:F} - \hat{V}_{1:F-1}) \in \mathbb{R}^{F \times N \times 2}.\]Motion Feature
To obtain compact motion features, the velocity and acceleration fields are further processed into spatial and temporal statistical histograms.
First, the magnitude and angle for each tracking point in the velocity and acceleration vector fields are computed respectively. Let $\rho(U)$ and $\phi(U)$ denote the magnitude and angle of a vector field $U$, where $U \in \mathbb{R}^{F \times N \times 2}$ and $U$ can be either $\hat{V}$ or $\hat{A}$.
\[\begin{aligned} \rho(U)_{i, j} &= \sqrt{U_{i,j,1}^2 + U_{i,j,2}^2}, &\forall i \in [F], j \in [N], \\ \phi(U)_{i, j} &= \left| \tanh^{-1}\left(\frac{U_{i, j,1}}{U_{i, j,2}}\right) \right|, &\forall i \in [F], j \in [N]. \end{aligned}\]Then, FVMD quantizes magnitudes and angles into discrete bins (8 for angles and 9 for magnitudes), which are then used to construct statistical histograms and extract motion features. It adopts dense 1D histograms
Dense 1D histograms are used for both velocity and acceleration fields, and the resulting features are concatenated to form a combined motion feature for computing similarity.
click here for 2D histogram construction
FVMD also explores quantized 2D histograms but opts to use the dense 1D histograms for the default configuration due to their superior performance. In this approach, the corresponding vector fields of each volume are aggregated to form a 2D histogram, where $x$ and $y$ coordinates represent magnitudes and angles, respectively. The 2D histograms from all volumes are then concatenated and flattened into a vector to serve as the motion feature. The shape of the quantized 2D histogram is $ \lfloor \frac{F}{f} \rfloor \times \lfloor \frac{\sqrt{N}}{k} \rfloor \times \lfloor \frac{\sqrt{N}}{k} \rfloor \times 72$, where the number 72 is derived from 8 discrete bins for angle and 9 bins for magnitude.Visualizations
If two videos are of very different quality, their histograms should look very different to serve as a discriminative motion feature. Let’s take a look at what they look like for the videos in real life.






Above, we show three pieces of video from the TikTok dataset
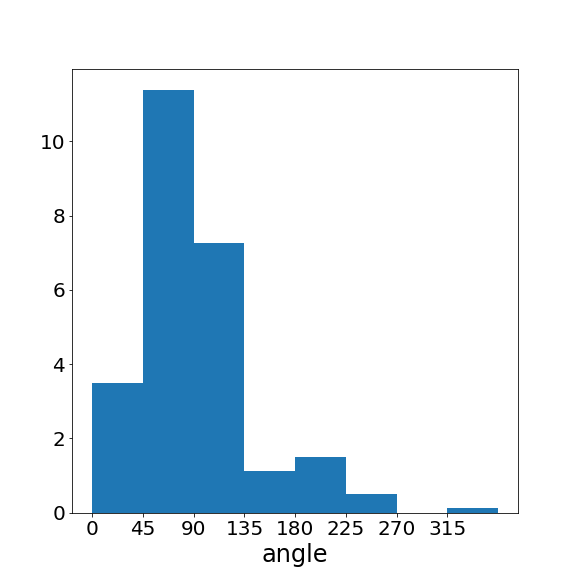
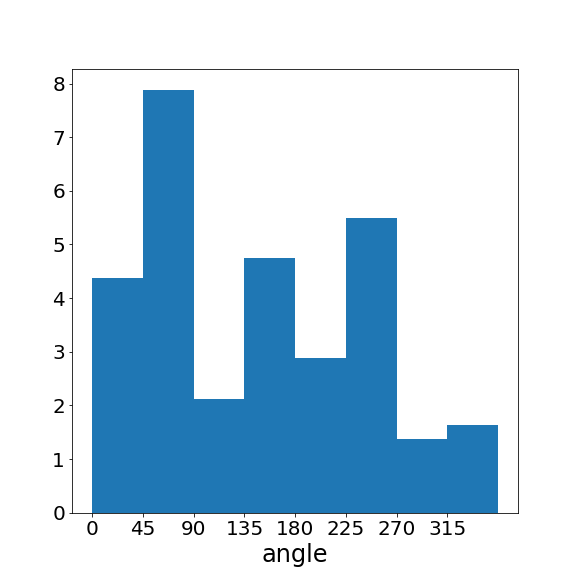
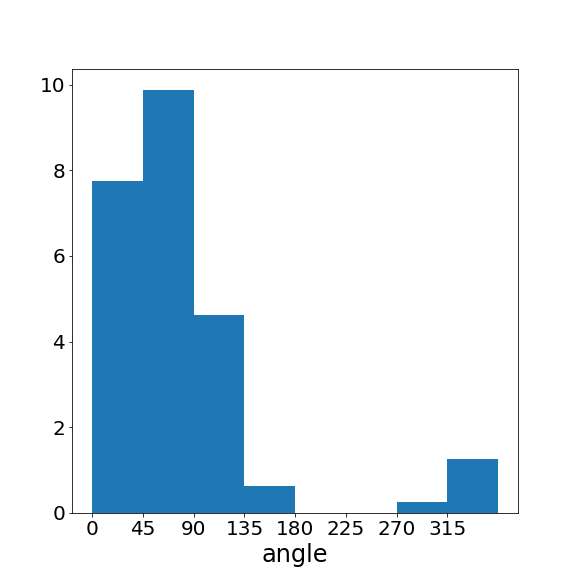
The low-quality video has more abrupt motion changes, resulting in a substantially greater number of large-angle velocity vectors. Therefore, the higher-quality video (right) has a motion pattern closer to the ground-truth video (left) than the lower-quality video (middle). This is exactly what we want to observe in the motion features! These features can capture the motion patterns effectively and distinguish between videos of different qualities.
click here for 2D histogram result
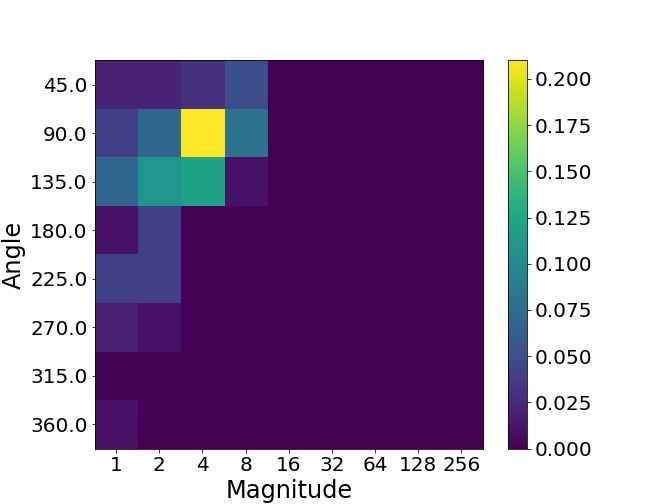
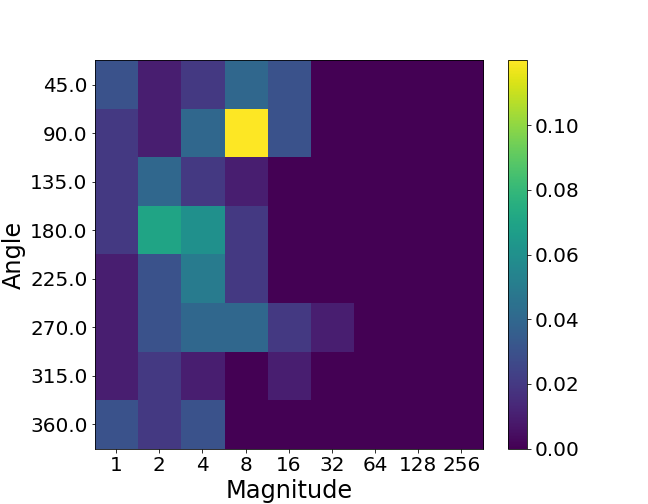
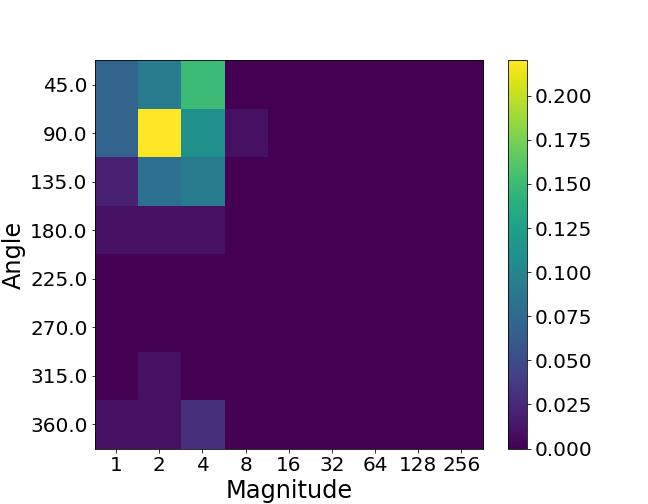
Fréchet Video Motion Distance
After extracting motion features from video segments of generated and ground-truth video sets, FVMD measures their similarity using the Fréchet distance
Experiments
The ultimate aim of a video evaluation metric is to align with human perception. To validate the effectiveness of FVMD, a series of experiments is conducted in the paper, including sanity check, sensitivity analysis, and quantitative comparison with existing metrics. Large-scale human studies are also performed to compare the performance of FVMD with other metrics.
Sanity Check
To verify the efficacy of the extracted motion features in representing motion patterns, a sanity check is performed in the FVMD paper. Motion features based on velocity, acceleration, and their combination are used to compare videos from the same dataset and different datasets.
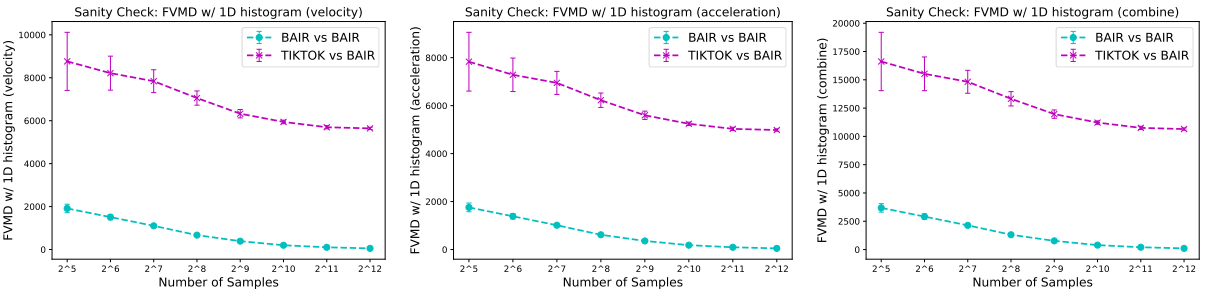
When measuring the FVMD of two subsets from the same dataset, it converges to zero as the sample size increases, confirming that the motion distribution within the same dataset is consistent. Conversely, the FVMD remains higher for subsets from different datasets, showing that their motion patterns exhibit a larger gap compared to those within the same dataset.
Sensitivity Analysis
Moreover, a sensitivity analysis is conducted to evaluate if the proposed metric can effectively detect temporal inconsistencies in generated videos, i.e., being numerically sensitive to temporal noises. To this end, artificially-made temporal noises are injected to the TikTok dancing dataset
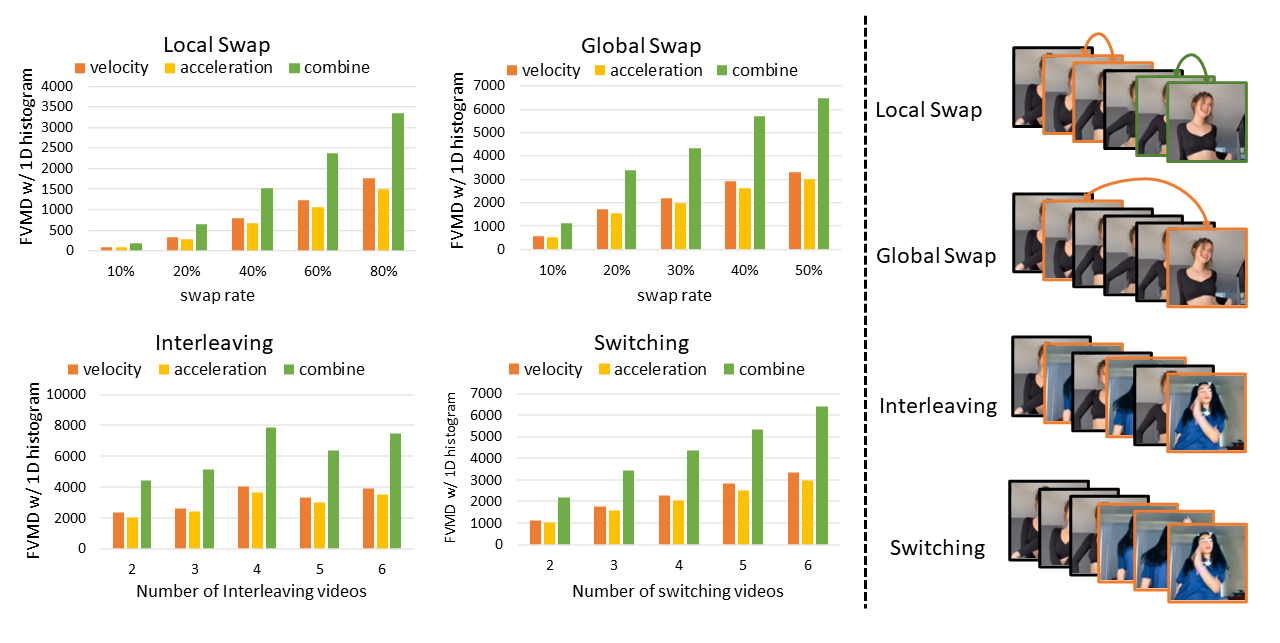
Across the four types of temporal noises injected into the dataset
Quantitative Results
Further, FVMD provides a quantitative comparison of various video evaluation metrics on TikTok dataset
| Metrics | Model (a) | Model (b) | Model (c) | Model (d) | Model (e) | Human Corr.↑ |
|---|---|---|---|---|---|---|
| FID↓ | 73.20 (3rd) | 79.35 (4th) | 63.15 (2nd) | 89.57 (5th) | 18.94 (1st) | 0.3 |
| FVD↓ | 405.26 (4th) | 468.50 (5th) | 247.37 (2nd) | 358.17 (3rd) | 147.90 (1st) | 0.8 |
| VBench↑ | 0.7430 (5th) | 0.7556 (4th) | 0.7841 (2nd) | 0.7711 (3rd) | 0.8244 (1st) | 0.9 |
| FVMD↓ | 7765.91 (5th) | 3178.80 (4th) | 2376.00 (3rd) | 1677.84 (2nd) | 926.55 (1st) | 1.0 |
FVMD ranks the models correctly in line with human ratings and has the highest correlation to human perceptions. Moreover, FVMD provides distinct scores for video samples of different quality, showing a clearer separation between models.
Human Study
In the paper, large-scale human studies are conducted to validate that the proposed FVMD metric aligns with human perceptions. Three different human pose-guided generative models are fine-tuned: DisCo
Following the model selection strategy in
The second setting, One Metric Diverse, evaluates the agreement among different metrics when a single metric provides a clear ranking of the performances of the considered video generative models. Specifically, model checkpoints whose samples can be clearly differentiated according to the given metric are selected to test the consistency between this metric, other metrics, and human raters.
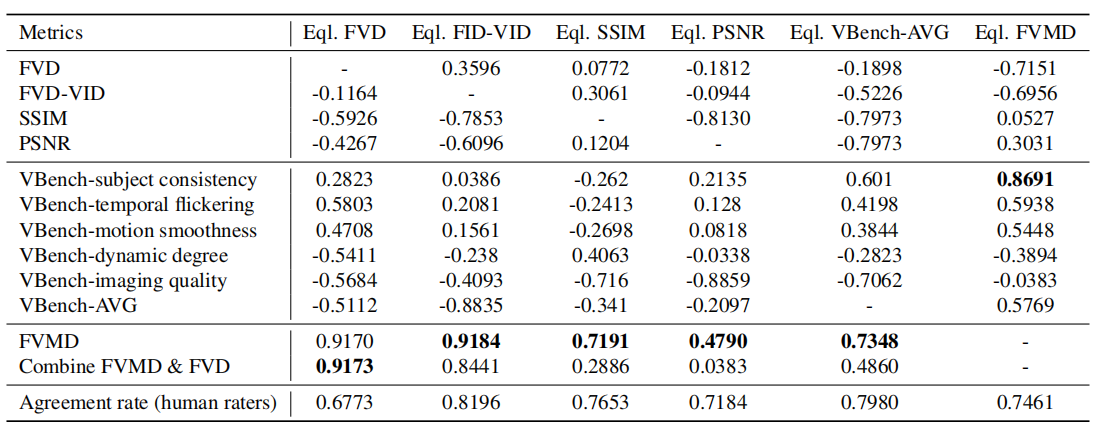
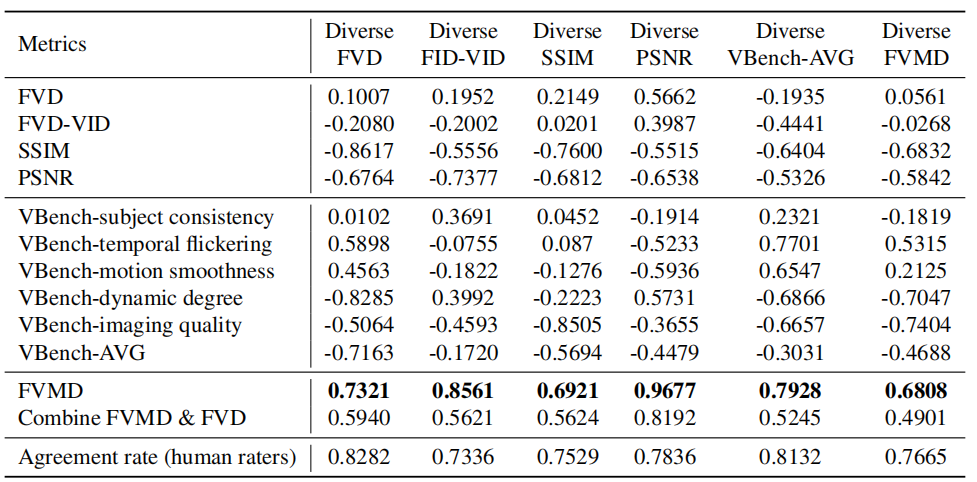
The Pearson correlations range in [-1, 1], with values closer to -1 or 1 indicating stronger negative or positive correlation, respectively. The agreement rate among raters is reported as a percentage from 0 to 1. A higher agreement rate indicates a stronger consensus among human raters and higher confidence in the ground-truth user scores. The correlation is higher-the-better for all metrics in both One Metric Equal and One Metric Diverse settings. Overall, FVMD demonstrates the strongest capability to distinguish videos when other metrics fall short.
Summary
In this blog, we give a brief summary of the recently-proposed Fréchet Video Motion Distance (FVMD) metric and its advantages over existing metrics. FVMD is designed to evaluate the motion consistency of generated videos by comparing the discrepancies of velocity and acceleration patterns between generated and ground-truth videos. The metric is validated through a series of experiments, including a sanity check, sensitivity analysis, quantitative comparison, and large-scale human studies. The results show that FVMD outperforms existing metrics in many aspects, such as better alignment with human judgment and a stronger capability to distinguish videos of different quality.